Knaster–Kuratowski–Mazurkiewicz lemma

The Knaster–Kuratowski–Mazurkiewicz lemma is a basic result in mathematical fixed-point theory published in 1929 by Knaster, Kuratowski and Mazurkiewicz in:

B. Knaster, C. Kuratowski, and S. Mazurkiewicz, Ein Beweis des Fixpunktsatzes für n-dimensionale Simplexe, Fund. Math. 14 (1929) 132–137.

The KKM lemma can be proved from Sperner's lemma and can be used to prove the Brouwer fixed point theorem.

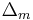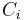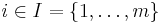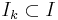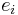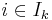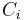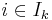KKM Lemma. Suppose that a simplex $\Delta_m$ is covered by the closed sets $C_i$ for $i \in I=\{1,\dots,m\}$ and that for all $I_k \subset I$ the face of S that is spanned by $e_i$ for $i \in I_k$ is covered by $C_i$ for $i \in I_k$ then all the 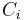$C_i$ have a common intersection point.

The two-dimensional case may serve as an illustration. In this case the simplex 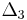$\Delta_3$ is a triangle, whose vertexes we can label 1, 2 and 3. 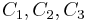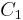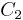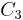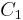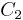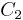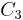We are given three closed sets $C_1,C_2,C_3$ which collectively cover the triangle; also we are told that $C_1$ covers vertex 1, $C_2$ covers vertex 2, $C_3$ covers vertex 3, and that the edge 12 (from vertex 1 to vertex 2) is covered by the sets $C_1$ and $C_2$ , the edge 23 is covered by the sets $C_2$ and $C_3$ , the edge 31 is covered by the sets 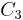$C_3$ and $C_1$ . 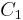The KKM lemma states that the sets 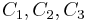$C_1, C_2, C_3$ have at least one point in common.

References

See the proof of KKM Lemma in Planet Math.